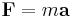Moment (physics)

Not to be confused with Momentum (physics).

For a more abstract concept of moments that evolved from this concept of physics, see Moment (mathematics).

Classical mechanics
$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics
Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics
Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Euler's laws of motion · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement
Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson

In physics, the term moment can refer to many different concepts:

Moment of force (often just moment) is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the force and the moment arm. The moment arm is the perpendicular distance from the point of rotation, to the line of action of the force. The moment may be thought of as a measure of the tendency of the force to cause rotation about an imaginary axis through a point.^[1] (Note: In mechanical and civil engineering, "moment" and "torque" have different meanings, while in physics they are synonyms. See the discussion in the "torque" article, or the article couple (mechanics).)

The moment of a force can be calculated about any point and not just the points in which the line of action of the force is perpendicular. Image A shows the components, the force F, and the moment arm, x when they are perpendicular to one another. When the force is not perpendicular to the point of interest, such as Point O in Images B and C, the magnitude of the Moment, M of a vector F about the point O is

$\mathbf{M_O} = \mathbf{r_{OF}} \times \mathbf{F}$

where

$\mathbf{r_{OF}}$ is the vector from point O to the position where quantity F is applied.

× represents the cross product of the vectors.^[2]

Image C represents the vector components of the force in Image B. In order to determine the Moment, M of a vector F about the point O, when vector F is not perpendicular to point O, one must resolve the force F, into its horizontal and vertical components. The sum of the moments of the two components of F about the point O is :

M _OF = F * sin (θ) * x + F * cos(θ) * 0

The moment arm to the vertical component of F is a distance x. The moment arm to the horizontal component of F does not exist. There is no rotational force about point O due to the horizontal component of F. Thus, the moment arm distance is zero, or 0.^[1]

Thus M can be referred to as "the moment M with respect to the axis that goes through the point O, or simply "the moment M about point O". If O is the origin, or, informally, if the axis involved is clear from context, one often omits O and says simply moment, rather than moment about O. Therefore, the moment about point O is indeed the cross product,

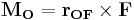$\mathbf{M_O} = \mathbf{r_{OF}} \times \mathbf{F}$ ,

since the cross product = F * x sin (θ)^[1]

When F is the force, the moment of force is the torque as defined above.

The Principle of moments is if an object is balanced then the sum of the clockwise moments about a pivot is equal to the sum of the anticlockwise moments about the same pivot.
A pure moment is a special type of moment of force. See the article couple (mechanics).
Moment of inertia ( 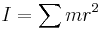$I = \sum m r^2$ ) is analogous to mass in discussions of rotational motion.
Moment of momentum or angular momentum ( 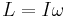$L = I \omega\!$ ) is the rotational analog of momentum.
Magnetic moment ( 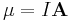$\mathbf{\mu}=I\mathbf{A}$ ) is a dipole moment measuring the strength and direction of a magnetic source.
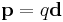Electric dipole moment is a dipole moment measuring the charge difference and direction between two or more charges. For example, the electric dipole moment between a change of -q and q separated by a distance of d is ( $\mathbf{p}=q \mathbf{d}$ )

External links

References

^ ^a ^b ^c Roberts, Adrian (2003). Statics and Dynamics with a Background in Mathematics. United Kingdom: The Press Syndicate of the University of Cambridge. pp. 1–300. ISBN 0521520878. http://books.google.com/books?id=DYPWQ-83xr8C&printsec=frontcover&dq=statics#v=onepage&q=moment&f=false.
^ Hall, A, S; Archer, F,E Gilbert, R,I (2005). Engineering Statics (Second ed.). Sydney, Australia: UNSW Press. pp. 39–227. ISBN 086840425. http://books.google.com/books?id=nsQd5r7J6WkC&printsec=frontcover&dq=statics#v=onepage&q=moment&f=false. Retrieved 2011-03-25.